이번에는 단순진자와 더불어 진동해석에서 가장 기초가 되는 모델인 '1자유도 비감쇠 시스템(스프링-질량 모델, spring-mass model)'에 대해 알아보겠습니다. 운동방정식 유도과정은 단순진자와 같습니다. 진동을 해석할 때 자주 등장하는 모델이므로, 같이 천천히 살펴보도록 하죠.
질량m을 가진 물체가 스프링을 통해 천장에 매달려 있습니다. 스프링에 매달린 물체는 위, 아래 방향으로만 움직이기 때문에 이 시스템은 '1자유도(single degree of freedom)'입니다. 여기서 중요한 것은 우리가 '선형'이라는 가정을 했기 때문에, 스프링은 '후크의 법칙(Hooke's law)'을 따른다고 가정합니다. 즉, 용수철은 선형 탄성 영역에서만 작용하는 것이죠. 따라서 스프링 상수를 k라고 하면, 스프링의 탄성력은 다음과 같습니다.

후크의 법칙은 아래 그림을 보면 쉽게 이해하실 겁니다.
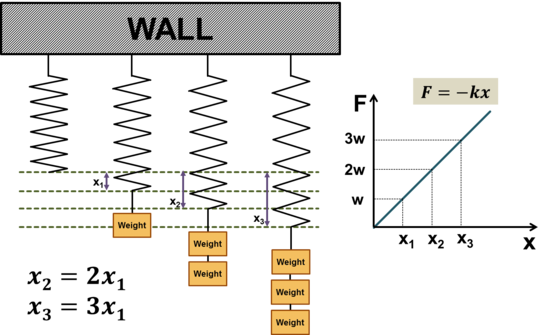
무게(weight)가 1단위 늘어날 때마다 변위도 일정하게 선형 비례합니다. 따라서 힘(=무게)과 변위 사이에는 k라는 기울기만큼 일정하게 비례하는 것이죠. 재료역학에서는 k를 '강성(stiffness)'이라고 부릅니다. 스프링 상수와 강성은 같은 의미입니다.
여담으로 많은 사람들이 '강성'과 '강도'를 헷갈려 하는데, '강성(stiffness)'은 변형에 저항하는 정도를 나타내고, '강도(strength)'는 파괴에 저항하는 정도를 나타냅니다. 따라서 강성과 강도의 단위도 다릅니다. 강성은 단위 길이 당 작용하는 힘이고, 강도는 단위 면적당 작용하는 힘입니다. 그러므로 어떤 제품을 설계할 때, 제품이 부서지는가는 강도에 대한 설계이고, 휘어지는가는 강성에 대한 설계입니다. 요즘 자동차 광고를 보면 '고장력강'을 많이 적용했다는 문구를 심심치 않게 볼 수 있는데, 고장력강은 일반적으로 인장강도(tensile strength)에 따라 분류되기 때문에 파괴에 대한 저항이 크다고 볼 수 있습니다.
이제 본격적으로 질량-스프링 모델의 운동방정식을 한 번 유도해보죠. 운동방정식은 두 가지 경우로 나눠서 구해보려고 합니다.
1. 첫 번째 경우
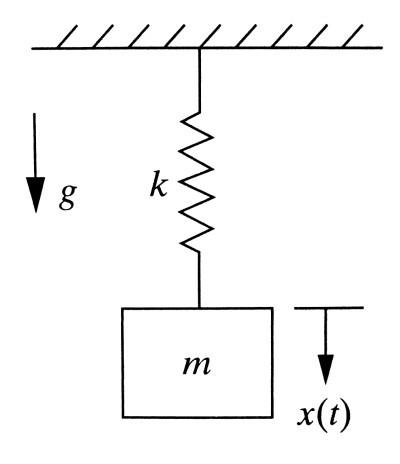
윗 그림과 같이 모형을 단순화했습니다. 강성k의 스프링과 질량m을 가진 물체를 달아놨습니다.

만약 스프링에 질량m물체를 설치하지 않았다면 그림(a)와 같습니다. 스프링에 아무것도 매달지 않은 상태의 스프링 길이를 '자유길이'라고 합니다. '자유길이'상태에서 여기에 질량m물체를 매달면 스프링 길이는 델타(Δ)만큼 증가해서 그림(b)와 같겠죠. 만약에 그림(b)에서 아무 힘도 작용하지 않은 '정적 평형 상태(static equilibrium state)'를 고려해보죠. (b)상태의 자유물체도는 다음 그림과 같습니다.

중력이 작용하는 방향(아래 방향)을 양(+)의 방향으로 설정하면, 정적 평형 상태이므로 다음과 같은 식을 얻을 수 있습니다. 여기서 많은 학생들이 스프링 힘이 작용하는 방향을 설정하는 것을 헷갈려하는데, 간단하게 생각하면 됩니다. 자유길이 상태에서 물체를 매달았기 때문에 스프링의 길이는 늘어납니다. 원래의 길이(자유길이)에서 늘어났기 때문에 스프링은 원래 상태로 되돌아가려는 힘을 질량m물체에 작용하겠죠. 즉 물체를 잡아당기려는 힘이 작용할 것 입니다. 반대로 만약에 양 손으로 스프링을 잡고 스프링 자유길이보다 더 수축시키면 스프링은 양 손에 밀어내려는 힘을 작용시킬 것 입니다. 이해가셨나요? 혹시나 아직도 헷갈린다면 다른 포스팅에서 또 설명하겠습니다. 따라서 자유물체도로부터 아래 식을 이끌어 낼 수 있습니다.

이제 그림(b)에서 중력 방향으로 어떤 힘이 작용했다고 하면, 자유길이에서 델타(Δ)의 변위에다가 x만큼 움직인 변위를 또 고려하면 되겠죠. 이때의 자유물체도는 다음과 같습니다.
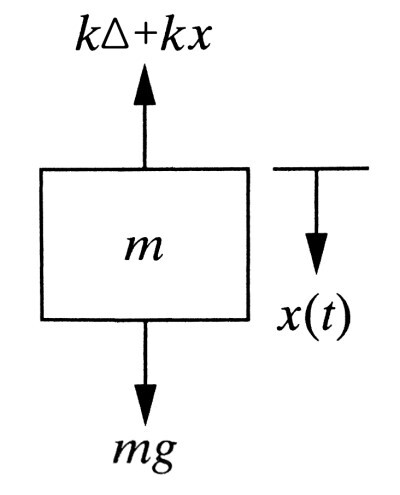
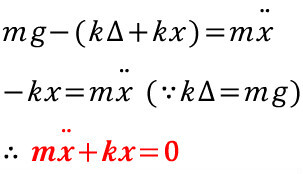
이렇게 스프링-질량 모델(1자유도 비감쇠 시스템)의 운동방정식을 유도했습니다. 이제 다른 상황에서의 스프링-질량 모델을 살펴보죠.
2. 두 번째 경우
이제는 천정에 스프링과 물체가 매달려 있는 상황이 아니라 다음 그림과 같이 고정된 벽면에 스프링과 질량m을 가진 물체가 평행하게 놓여있는 상황입니다.
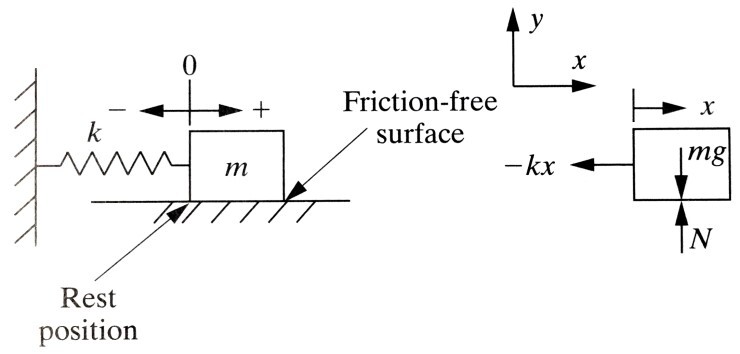
자유물체도로 부터 운동방정식을 유도해봅시다. x축 방향으로 물체가 거동을 했다면,
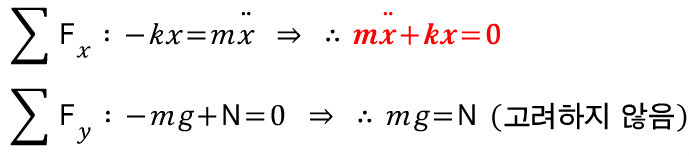
두 번째 경우에서 얻은 운동방정식은 꽤나 간단하게 구했습니다. 그럼 애초에 운동방정식을 유도할 때 두 번째 경우를 고려하면 되지 왜 번거롭게 두 개의 상황을 나눠서 살펴봤느냐하면, 천장에 스프링과 물체가 매달려도 중력의 영향을 받지 않는다는 것을 보여주기 위해서입니다.
이렇게 스프링-질량 모델의 운동방정식을 유도해봤습니다. 다음 포스팅에서는 1자유도 비감쇠 시스템의 해(응답)를 구해보도록 하겠습니다.
댓글