이번에는 지반 가진(또는 바닥 가진, base excitation, seismic excitation)에 대한 설명을 하려고 합니다. 지반 가진은 앞서 다뤄봤던 조화 가진의 응용입니다.
바로 전 까지는 물체 m에 힘이 가해졌을 때의 상황을 묘사했다면, 지반 가진은 말 그대로 물체을 지지하는 벽 또는 바닥이 흔들릴 때의 상황을 묘사한 것입니다. 지반 가진으로 모델링할 수 있는 경우가 바로 지진입니다. 지진은 땅이 흔들리면서 건물에 힘을 가하는 것이죠. 또 지반 가진은 울퉁불퉁한 땅을 달리는 자동차를 묘사할 수 있습니다. 자동차가 비포장도로를 달릴 때, 차는 위아래로 진동을 하게 됩니다. 여기서 다루는 지반 가진은 지반(base)이 위, 아래로 힘이 가해질 때를 나타냅니다. 지진은 일반적으로 횡(옆으로)으로 움직이기 때문에 적절하지 않지만, 기본적인 개념은 같습니다.
그럼 지반 가진에서의 운동방정식을 구해봅시다.
만약 물체 m은 평형상태에 있는데, 갑자기 지반이 위로 움직였다고 생각해보죠. 물체m의 변위를 x, 지반이 움직이는 변위를 y라고 할 때, 물체와 지반사이의 변위는 항상 (x-y)가 됩니다. 지반이 일정한 주기를 가지고 계속 움직인다고 생각해 봅시다. 이때 일정한 주기로 움직이는 지반이 가하는 힘은 다음과 같이 표현할 수 있습니다.

윗 그림의 자유물체도 (b)로 부터 운동방정식을 유도해 봅시다.

윗 식의 우변을 보면 항이 두 개가 있습니다.
따라서 특수해를 두 번 구해야(...)합니다. 귀찮겠지만 한 번 구해봅시다.
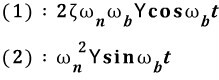
(1) 첫 번째 특수해
첫 번째 특수해 (1) 를 구해볼까요? 우선 특수해를 다음과 같다고 가정합시다.

특수해가 복소수로 이루어졌다고 가정하면, 복소수에서 실수부분이 첫 번째 특수해가 되는 것입니다. 복소수로 이루어진 해를 미분해 봅시다.
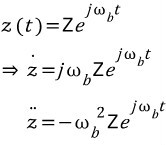
윗 식을 운동방정식에 대입하면,

첫 번째 특수해는 복소수로 이루어진 해의 실수 부분이기 때문에, 오일러 공식에 의해 cos은 복소수의 실수 부분이고, 다시 cos은 복소수로 표현할 수 있습니다. 그래서 cos에서 e^(jωt)로 나타냈습니다. 어차피 나중에 실수부분만 표현하면 되기 때문에 복소수로 나타내도 전혀 문제되지 않습니다.

복소수에서 오일러 공식으로 표현한 과정은 아래를 참고하면 이해되리라 봅니다.


따라서 우리가 구할 첫 번째 특수해는 다음과 같습니다.

(2) 두 번째 특수해
이제 두 번째 특수해를 구해봅시다. 두 번째 특수해는 다음과 같이 가정합니다.

마찬가지로 운동방정식에 대입합니다.

두 번째 특수해는 복소수로 이루어진 해의 허수 부분이기 때문에, 오일러 공식에 의해 sin은 복소수의 허수 부분이고, 다시 sin은 복소수로 표현할 수 있습니다. 그래서 sin을 e^(jωt)로 나타냈습니다. 어차피 나중에 허수 부분만 표현하면 되기 때문에 복소수로 나타내도 전혀 문제되지 않습니다.

따라서 우리가 구할 두 번째 특수해는 다음과 같습니다.

우리가 다루는 시스템은 선형시스템이므로 중첩의 원리를 적용한 최종적인 특수해는 다음과 같습니다.

아직 끝이 아닙니다. 이번 포스팅은 여기서 잠깐 쉬고, 다음 포스팅에서 계속 이어가겠습니다.




댓글